LABOMATHS 2C | Mathématiques 71

Domaine: résolution de problèmes

La schématisation en barres

Les membres du Labomaths 2C ont choisi d’initier leurs élèves à la schématisation en barres en résolution de problèmes.

La schématisation en barres permet de représenter tous les types de problèmes (basiques mais aussi complexes, et parfois atypiques) de manière simple, sans multiplier les différentes sortes de schémas.

L’initiation doit commencer avec des problèmes dont le schéma en barres correspondant soit congruent avec l’énoncé afin que les élèves visualisent facilement la situation du problème, c’est le cas avec les problèmes de composition par exemple ( voir les expériences menées en classe).

Deux groupes ont travaillé simultanément, l’un pour le cycle 2, l’autre pour le cycle 3. Pour cela, ils se sont inspirés de la Démarche pour résoudre des problèmes arithmétiques au cycle 2 élaborée par les référentes mathématiques du département du Rhône, ainsi que la Banque de problèmes cycle 3, annexe de la démarche ci-dessus.

Chaque enseignante a construit une séance de résolution d’un problème de référence dont l’objectif principal est d’initier les élèves au schéma en barres. Afin de ne pas mettre les élèves en difficulté et leur permettre de se concentrer sur la schématisation, les problèmes choisis sont relativement simples. Nous avons fait le choix de ne pas imposer une séance type pour toutes les classes afin d’explorer diverses pistes d’approche du schéma, en respectant toutefois les incontournables tels que la dévolution, la résolution individuelle, la mise en commun, l’institutionnalisation et le réinvestissement.

Guide Pour enseigner les nombres, le calcul et la résolution de problèmes au CP, MEN:

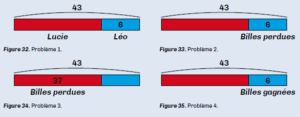
« Ce type de schéma en barres va notamment aider les élèves à reconnaître les structures mathématiques des problèmes, les opérations et procédures sous-jacentes grâce à l’analogie visuelle entre les représentations schématiques utilisées. Un grand avantage de cette modélisation réside dans le fait que les problèmes basiques peuvent ainsi prendre la même forme schématique et correspondre au même « modèle ». Par exemple, les quatre problèmes suivants se ramènent au même type de schéma:
1. Léo et Lucie ont 43 billes à eux deux. Léo a 6 billes. Combien Lucie a-t-elle de billes ?
2. Lucie avait 43 billes ce matin. Elle a perdu 6 billes pendant la récréation. Combien a-t-elle de billes maintenant ?
3. Lucie avait 43 billes ce matin. Elle a perdu 37 billes pendant la récréation. Combien a-t-elle de billes maintenant ?
4. Lucie a gagné 6 billes à la récréation. Maintenant elle a 43 billes. Combien de billes avait-elle avant la récréation ?