Nous avons choisi de travailler en résolution de problèmes avec un problème atypique ouvert∗, Des bananes dans le désert, qui peut être adapté selon le niveau des élèves:

Problème initial: Dans un désert d’une longueur de 1000 km, vous devez transporter 3000 bananes avec un dromadaire ne pouvant porter que 1000 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, quel est le plus grand nombre de bananes que vous pouvez apporter au bout du désert ?
Cycle 3: Dans un désert d’une longueur de 100 km, vous devez transporter 300 bananes avec un dromadaire ne pouvant porter que 100 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, quel est le plus grand nombre de bananes que vous pouvez apporter au bout du désert ?
Cycle 2 et 3: Dans un désert d’une longueur de 10 km, vous devez transporter 30 bananes avec un dromadaire ne pouvant porter que 10 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, comment faire pour emmener 4 bananes à l’autre bout du désert ?
Problèmes similaires avec une modélisation identique (multiprésentations):
|
Un écureuil change de cachette car elle est trop petite. Il faut qu’il emporte ses 300 noisettes dans sa nouvelle cachette située dans un arbre à 100 m. Il ne peut porter que 100 noisettes sur son dos mais étant gourmand il a besoin de manger une noisette par mètre parcouru. Quel est le plus grand nombre de noisettes qu’il peut emporter dans sa nouvelle cachette ? Un kangourou doit emporter 300 kiwis à son petit de l’autre côté de la prairie. La prairie se traverse en 100 bonds. Il ne peut transporter que 100 kiwis dans sa poche mais à chaque bond il perd un kiwi qui s’écrase par terre. Quel est le plus grand nombre de kiwis entiers qu’il peut emporter à son petit ? Problèmes adaptés au cycle 2 (CP) : Au zoo, dans l’enclos du singe, il y a 4 arbres en ligne. Dans le premier arbre il y a 6 bananes. Le singe doit transporter 1 banane sur le dernier arbre. Mais attention ! Le singe ne peut porter que 3 bananes à la fois et à chaque fois qu’il fait un saut, il doit manger une banane pour prendre des forces ! Combien de bananes peut-il emporter sur le dernier arbre ? Au zoo, dans l’enclos du singe, il y a 10 arbres en ligne. Dans le premier arbre il y a 20 bananes. Le singe doit transporter le plus de bananes sur le dernier arbre. Mais attention ! Le singe ne peut porter que 10 bananes à la fois et à chaque fois qu’il fait un saut, il doit manger une banane pour prendre des forces ! Combien de bananes peut-il emporter sur le dernier arbre ? Dans la jungle, un singe veut ramener le plus possible de bananes. Il y a 20 bananes sur un bananier. Pour retourner chez lui, le singe doit sauter sur 10 rochers. Mais attention ! Le singe ne peut porter que 10 bananes à la fois et à chaque fois qu’il fait un saut, il doit manger une banane pour prendre des forces. Combien de bananes le singe peut-il emporter chez lui ? Remarques importantes: Ces problèmes sont difficiles à mettre en place dans les classes, de nombreux imprévus, souvent liés à l’interprétation des énoncés par les élèves, apparaissent au fur et à mesure des tests. Ces énoncés ont été modifiés très régulièrement au cours des expériences et nécessitent d’être testés à nouveau afin d’optimiser les séances. ∗ problème de type ouvert: on peut définir cette catégorie de problèmes comme des situations dont l’énoncé n’induit ni méthode ni application immédiate, mais dont le contexte est suffisamment familier des élèves pour qu’ils puissent entrer rapidement dans la recherche et faire des hypothèses. Ces problèmes peuvent avoir des solutions encore difficiles à prouver en mathématiques. Thierry Dias |
Rappel des programmes corrigés 2018 :
« Aux cycles 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »
Tout en privilégiant la manipulation, la verbalisation et l’abstraction, nous avons pris soin de proposer des pistes de remédiation et d’extension afin que chaque élève puisse évoluer selon son rythme.
 <Schématisation faite avec des CM1 (30 bananes dans le désert)
<Schématisation faite avec des CM1 (30 bananes dans le désert)
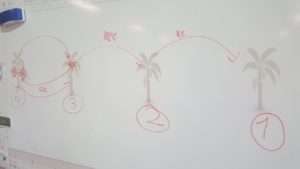
Schématisation test du problème 6 bananes pour le singe CP ^
Matériel:
Fiche de séance BANANES DANS LE DÉSERT
30 Bananes dans le désert C2C3
30 Bananes dans le désert C2 V2
Grilles d’analyse des séances expérimentées dans les classes en co-observation:
Lien vers la solution du problème initial (désert de 1000km)
VIDÉOS (mot de passe: labomaths):
LBM C1 Classe de CM1 de Vincent
LBM C2 Classe de CP d’Anne-Sophie
