Tous les articles par ogenelot
Mesures Cycle 3
LABOMATHS 2.5
Domaine: résolution de problèmes
En raison de l’épidémie de Covid 19, de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.
LABOMATHS 2.4 – cycle 1
Le jeu de la marchande : construction du nombre
Domaine: structurer sa pensée

Les membres du Labomaths 2.4 ont souhaité travailler la composition et la décomposition des premiers nombres à partir du jeu de la marchande, de la PS à la GS. Pour cela, l’idée phare était de partir du réel, notamment emmener sa classe au marché ou dans un commerce pour mettre les enfants en situation concrète. Cela a permis de travailler, outre la construction du nombre, le langage et la manipulation de la monnaie.
Vous trouverez ci-dessous trois séquences: une en petite section, une en moyenne section, une en grande section. Pour chaque séquence, une séance testée en classe est détaillée, pour chaque niveau de maternelle.
Extraits du BO du 18 février 2015, programme d’enseignement de l’école maternelle:
« Le jeu favorise la richesse des expériences vécues par les enfants dans l’ensemble des classes de l’école maternelle et alimente tous les domaines d’apprentissage. Il permet aux enfants d’exercer leur autonomie, d’agir sur le réel, de construire des fictions et de développer leur imaginaire, d’exercer des conduites motrices, d’expérimenter des règles et des rôles sociaux variés. […] L’enseignant propose des jeux structurés visant explicitement des apprentissages spécifiques. »
« Pour provoquer la réflexion des enfants, l’enseignant les met face à des problèmes à leur portée […] il cible des situations […] il est attentif aux cheminements qui se manifestent par le langage ou en action. »
« Les trois années de l’école maternelle sont nécessaires […] pour stabiliser les connaissances (sur le nombre) en veillant à ce que les nombres travaillés soient composés et décomposés. La maîtrise de la décomposition des nombres est une condition nécessaire à la construction du nombre. »
Petite Section :
PS Séance 5 détaillée marchande
Moyenne Section :
MS Séance 5 détaillée marchande
Grande Section :
GS Séance 6 détaillée marchande
Tous les documents fusionnés en pdf :
Vidéo filmée dans la classe de GS de Marie-Christine Boyer, école de l’Est, Chalon 2 :
LABOMATHS 2.3
Jeux mathématiques pour travailler les compléments
Domaines: numération et calcul mental
Lors de l’année 2018-2019, les enseignantes de l’ex-LaboMaths D avaient travaillé sur la numération de position, et notamment élaboré des jeux de Loto afin de consolider les notions de chiffre et de nombre chez des élèves de cycle 2 et 3. Cette année, les membres du groupe ont désiré poursuivre leur travail collaboratif en axant leur thématique autour du calcul mental et en travaillant plus précisément les compléments à dix et aux dizaines supérieures. Les jeux élaborés s’adressent à des élèves de cycle 2, mais les élèves de cycle 3 peuvent en bénéficier: renforcement pour des élèves en difficulté, consolidation pour les autres.
BO n° 30 du 26/07/2018 (extraits):
« La pratique quotidienne du calcul mental conforte la maîtrise des nombres et des opérations et permet l’acquisition d’automatismes procéduraux et la mémorisation de résultats comme ceux des compléments à 10, des tables d’addition et de multiplication. »
Repères annuels de progression du cycle 2:

Les élèves ont travaillé les compléments à l’aide de jeux de calcul mental élaborés par le Labomaths 2.3:
- le jeu Cache 10 inspiré du jeu Les Dix-minos (Ermel CE1) testé en classe de CP et CE1.
- le jeu La Rivière aux Dizaines testé avec des petits groupes de CE2, CM1 et CM2.
CACHE 10
pour travailler essentiellement les compléments à dix (cycle 2)
Remarques:
- Attention au découpage des cartes: chacune doit regrouper deux cases (comme un domino).
- Prévoir 5 caches de chaque taille pour chaque élève et des couleurs différentes par joueur.
Vidéo: Classes de CE1 CE2 de Magali et CE1 de Bénédicte (mot de passe labomaths71)
—————————-
La Rivière aux Dizaines
pour travailler les compléments aux dizaines supérieures et le calcul mental (cycle 3)
LABOMATHS 2.2
La schématisation
Domaine: résolution de problèmes
Après un travail conséquent sur les typologies de problèmes selon Catherine Houdement et Gérard Vergnaud, le groupe Labomaths s’est attardé sur la conférence de Serge Petit (professeur honoraire de mathématiques, IUFM d’Alsace) intitulée Résolution de problèmes et registres de représentations sémiotiques.
Après un visionnage attentif de cette conférence, entrecoupée d’échanges constructifs, le groupe a décidé d’orienter le travail du Labomaths vers la schématisation en RDP. De nombreuses questions émergent: comment faire pour que le schéma soit un outil à la résolution de problèmes ? Comment l’introduire ? Quels problèmes travailler ? Problèmes basiques ? Complexes ? Faut-il se concentrer sur les problèmes qui mettent en jeu une chronologie, une notion de temps ? Certains élèves ont déjà des représentations schématiques, cela peut-il servir d’amorce pour en trouver d’autres ? Comment travailler les représentations sémiotiques dans les classes (CE et CM) ?
Lien vers le site de l’Académie des Sciences pour visionner la conférence de Serge Petit
En raison de l’épidémie de Covid 19 et de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.
LABOMATHS 2.1
Résolution d’un problème atypique
Les 99 carrés
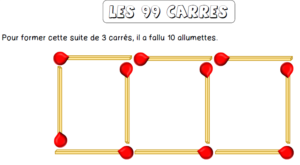
Après un travail conséquent sur la catégorisation de problèmes selon Catherine Houdement et Gérard Vergnaud, les enseignant.e.s du Labomaths 2.1 ont choisi de faire résoudre un problème de recherche à leurs élèves, les 99 carrés, en s’inspirant des recherches faites par le laboratoire 3LS (Laboratoire Lausannois Lesson Study) dirigé par Stéphane Clivaz, professeur spécialiste de la didactique des mathématiques à la Haute École Pédagogique du canton de Vaud.
Rappel des programmes corrigés 2018 :
« Aux cycles 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »
Compte-rendu de la dernière réunion avant le confinement
Plan leçon des 99 carrés, labo 3LS HEP Vaud
En raison de l’épidémie de Covid 19, de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.
LABOMATHS 2.6
PROJET BAR-NUM
Domaine: numération
Le jeu Bar-Num a été élaboré par les maîtres sur-numéraires de Chalon 2 à partir du jeu des « frites » (de piscine) proposé par la Méthode Heuristique des Maths (MHM) de Nicolas Pinel, Inspecteur de l’Education Nationale. Il permet de travailler les compositions et les décompositions des premiers nombres de 1 à 10 avec des élèves de cycle 1 et début cycle 2.


En raison de l’épidémie de Covid 19, de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.
LABOMATHS 1.3
Grandeurs et mesures: les masses
Comment travailler les représentations avec des unités non usuelles ?

Les enseignantes de ce groupe ont souhaité travailler les représentations des grandeurs et en particulier les masses. Elles remarquent régulièrement que leurs élèves ont des difficultés à se représenter ce qu’est un mètre, un kilomètre, un kilogramme, un litre, etc … Dans ce domaine, en cycle 2, on a tendance à travailler très vite avec les unités de mesures usuelles, alors que beaucoup d’élèves ont encore besoin de manipuler, de « voir », de « sentir », de « soupeser » ce que fait un kilogramme, de se rendre compte d’une distance « en vrai », de comparer différents objets en les soupesant, … Ce travail est la plupart du temps pratiqué en classe, mais peut-être pas suffisamment pour certains élèves.
Les enseignantes font remarquer que les élèves manipulent peu, qu’on va souvent trop vite pour répondre aux demandes institutionnelles. La manipulation est utile seulement si les élèves apprennent quelque chose, si elle a un objectif. On ne manipule pas sans but : attention au mode « énactif » ; la manipulation n’est pas un « jeu », elle doit permettre de faire émerger une notion, un savoir, d’où la difficulté pour trouver des situations qui permettent cette manipulation…
Le groupe décide de s’orienter plutôt vers les mesures de masses pour travailler les notions d’estimation et d’étalonnage avec des manipulations d’objets de masse identiques ou différentes, et des pesées avec des unités non usuelles. Le visionnage de l’intervention de Céline Mousset et d’Hélène Gagneux sur les grandeurs et mesures lors du colloque organisé par l’ Académie des Sciences en décembre 2018 a beaucoup aidé dans ce choix.
Repères annuels : « Les élèves comparent des objets selon leur masse, en les soupesant puis en utilisant la balance à plateaux, type Roberval, sans que des unités de mesure soient nécessairement introduites. Ils donnent du sens aux expressions : « Plus lourd que, plus léger… ».
Attendus de fin de CP
Ce que sait faire l’élève:
– Il compare des objets selon leurs masses, en les soupesant (si les masses sont suffisamment distinctes) ou en utilisant une balance de type Roberval.
-Il utilise le lexique spécifique associé aux masses: plus lourd, moins lourd, plus léger.
Exemples de réussite: les situations s’appuient toutes sur des manipulations
Il compare les masses de deux objets par comparaison directe et indirecte à l’aide d’une balance.
Parmi deux ou trois bouteilles opaques d’apparence identique, mais remplies différemment (l’objectif est qu’elles aient des masses différentes), il sait dire laquelle est la plus lourde ou laquelle est la plus légère.
Attendus de fin de CE1 et de CE2
Il sait identifier l’objet le plus léger (ou le plus lourd) parmi 2 ou 3 objets de volume comparable en les soupesant ou en utilisant une balance.
Il compare des masses par comparaison directe et indirecte à l’aide d’une balance.
Il estime un ordre de grandeur en référence à certains objets du quotidien.
Pour comparer deux masses, il utilise le vocabulaire approprié.
Compte-rendu de la dernière réunion du Labomaths avant le confinement
En raison de l’épidémie de Covid 19 et de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.
LABOMATHS 1.2
PROJET AVDV (Application Verger De Village)
Domaines: Résolution de problèmes, grandeurs et mesures
 |
|
Le projet initial du Labomaths 1.2 était de travailler la résolution de problèmes à partir de données issues du terrain, le verger du village de La Charmée, où de nombreux arbres fruitiers sont visités régulièrement par les élèves du RPI regroupant les écoles de Granges, Saint Germain-les-Buxy et La Charmée.
A partir de mesures prises dans le verger, les élèves de cycle 2 et 3 auraient dû résoudre des problèmes correspondant à leurs niveaux de classe. En raison de l’épidémie de covid 19 et de la fermeture des écoles en mars 2020, nous n’avons pas pu finaliser le projet. Seules les mesures sur le terrain et leur exploitation dans les classes ont été réalisées, ce qui a déjà demandé beaucoup de temps de préparation et d’organisation. Les enseignant.e.s envisageaient de faire résoudre un problème de recherche aux élèves de chaque cycle à partir d’une commande fictive de la mairie. Cette commande se serait présentée sous forme d’une lettre précisant que la municipalité souhaitait entourer le verger d’un grillage, avec un portillon et un portail. Les élèves auraient été chargés de réaliser un devis à l’aide de catalogues papier ou en ligne, puis d’écrire un problème collectif dans le but de le proposer à une classe d’une autre commune. Cette phase n’a pu être réalisée, les conditions de réouverture des écoles en mai 2020 n’étaient pas propices à ce type de travail qui aurait demandé une coopération étroite entre élèves. En accord avec les enseignant.e.s, cette phase sera reportée au premier trimestre de l’année scolaire 2020-2021.
Les données recueillies sur le terrain ont été transmises à deux étudiants de l’IUT de Chalon afin qu’ils réalisent une application en réalité virtuelle dans le cadre de leur parcours de master.
Voir le projet pensé au niveau des étudiants
BO n° 30 du 26/07/2018 (extraits):
« Au cycle 2, la résolution de problèmes est au centre de l’activité mathématiques des élèves […]. Les problèmes […] peuvent être issus de situations de vie de classe ou de situations rencontrées dans d’autres enseignements, notamment « Questionner le monde », ce qui contribue à renforcer le lien entre les mathématiques et les autres disciplines. […] L’étude des quatre opérations commence dès le début du cycle à partir de problèmes qui contribuent à leur donner du sens, en particulier des problèmes portant sur des grandeurs ou sur leurs mesures. […] En lien avec le travail mené dans « Questionner le monde » les élèves rencontrent des grandeurs qu’ils apprennent à mesurer […]. L’étude des grandeurs et de leurs mesures doit faire l’objet d’un enseignement structuré et explicite qui s’appuie sur des situations de manipulation. »
Repères annuels de progression Grandeurs et mesures pour le cycle 2:

BO n° 25 du 21/06/2018:
« Dans la continuité des cycles précédents, le cycle 3 assure la poursuite du développement des six compétences majeures des mathématiques: chercher, modéliser, représenter, calculer, raisonner et communiquer. La résolution de problèmes constitue le critère principal de la maîtrise des connaissances dans tous les domaines des mathématiques […]. Les situations sur lesquelles portent les problèmes sont, le plus souvent, issues de la vie de classe, de la vie courante ou d’autres enseignements, ce qui contribue à renforcer le lien entre les mathématiques et les autres disciplines. »
Repères annuels de progression Grandeurs et mesures pour le cycle 3:

|
|
|
|
|
|
 |
|
Phase 2 du projet: résolution de problème à partir d’une commande fictive de la mairie
Vidéo: mesure de distances entre les arbres avec deux petites cordes identiques par des CP CE1:






