Tous les articles par ogenelot

LABOMATHS 1.1

11 juin 2019 ogenelot

Domaine: Résolution de problèmes

Objectif Dix

La résolution de problème est la thématique du groupe. Nous avons choisi de travailler les analogies entre problèmes en se basant sur les préconisations en RDP d’instituer 10 problèmes par semaine sur l’ensemble de la scolarité élémentaire. Nous avons été inspirés par les travaux réalisés par Nicolas Naulin (PEMF) dans sa classe de CM2 dans la circonscription de Charolles (merci à lui pour ses conseils et informations diverses !) et avons souhaité adapter son procédé à des classes de cycle 2 (CP, CE1 et CE2). Devant l’ampleur du travail, nous avons tout d’abord construit un protocole sur une semaine type avant de l’enrichir progressivement pour tenter de couvrir quatre semaines selon une programmation basée sur les différentes typologies de problèmes (selon G. Vergnaud et C. Houdement). Un travail approfondi sur les énoncés des problèmes a été mené en s’inspirant des travaux de Stella Baruk et Serge Petit. Lors des résolutions, les élèves ont été initiés à la schématisation de problèmes basiques: certains schémas leur ont été proposés par les enseignantes, d’autres viennent des élèves eux-mêmes.

Le protocole Objectif 10:

Lundi: un problème de référence (résolution / institutionnalisation)

Mardi: trois problèmes dont un problème analogue à celui du lundi (contexte identique au lundi, données numériques différentes)

Jeudi: trois problèmes dont un problème analogue à celui du lundi (contextes différents, données numériques identiques au lundi)

Vendredi: trois problèmes dont un problème analogue à celui du lundi (contextes différents, données numériques différentes)

BO n° 30 du 26/07/2018 (extrait):

« Au cycle 2, la résolution de problèmes est au centre de l’activité mathématiques des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions, de provoquer des questionnements. Ils peuvent être issus de situations de vie de classe ou de situations rencontrées dans d’autres enseignements, notamment « questionner le monde », ce qui contribue à renforcer le lien entre les mathématiques et les autres disciplines. Il ont le plus souvent possible un caractère ludique. […] »

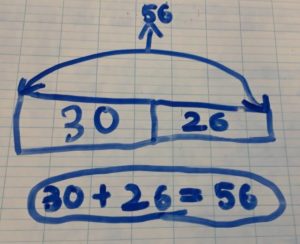
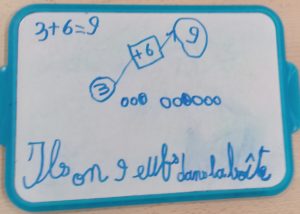
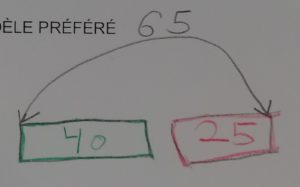
Exemples de schémas de CE1

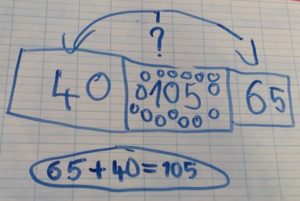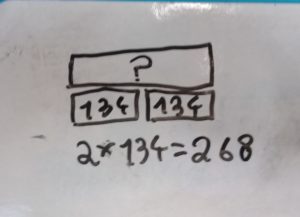
Exemples de schémas de CE2

GRILLE PRÉPARATION CP

GRILLE PRÉPARATION CE1CE2

GRILLE OBSERVATION ANALYSE CP

GRILLE OBSERVATION ANALYSE CE1

GRILLE OBSERVATION ANALYSE CE2

LA SCHEMATISATION EN CYCLE 2

Quatre semaines de problèmes en CP

Quatre semaines de problèmes en CE1

Quatre semaines de problèmes en CE2

En raison de l’épidémie de COVID 19 et de la fermeture des écoles en mars 2020, les problèmes n’ont pas tous été testés dans les différentes classes. Il se peut que certains de ces problèmes, notamment ceux des semaines 4, aient besoin d’ajustements, ajustements qui auraient dû se faire à la suite des tests dans les classes.

LABOMATHS

LaboMaths D

6 mai 2019 ogenelot

Nous avons choisi de consolider la numération décimale de position et la signification de la place des chiffres dans les nombres inférieurs à 1000 ( dans 108, il n’y a pas 0 dizaine mais 10 dizaines , distinction entre le chiffre des … et le nombre de … ) en privilégiant le cycle 2. Deux jeux différents ont été testés dans des classes de CP, CE et CM: le jeu de Loto Coopératif et le jeu du manège (adaptation du jeu de la toupie élaboré par le laboratoire 3LS de la HEP de Lausanne).

Rappel des programmes corrigés 2018:

« Au cycle 2, les élèves consolident leur compréhension des nombres entiers, déjà rencontrés au cycle 1. Ils étudient différentes manières de désigner les nombres, notamment leurs écritures en chiffres, leurs noms à l’oral, les compositions-décompositions fondées sur les propriétés numériques, ainsi que les décompositions en unités de numération (unités, dizaines, etc.). »

Tout en privilégiant la manipulation, la verbalisation et l’abstraction, nous avons pris soin de proposer des pistes de remédiation et d’extension afin que chaque élève puisse évoluer selon son rythme.

Matériel:

Fiche de séance LE LOTO COOPERATIF

>LOTO DES CP EXERCICES LOTO CP

>LOTO DES CE EXERCICES LOTO CE

>LOTO DES CM EXERCICES LOTO CM

>Jeu du manège CP >Jeu du manège CECM

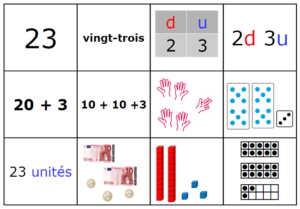
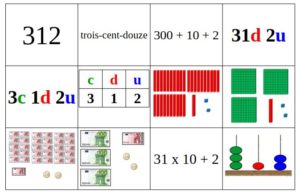
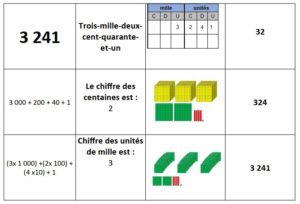
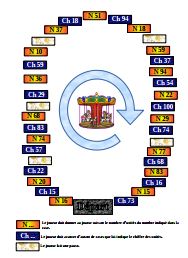
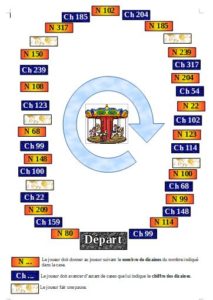
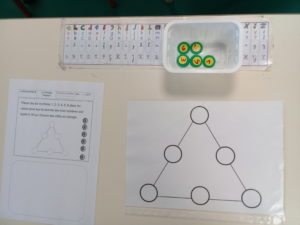
Matériel de numération version papier avec la grille grand format^

Matériel numération version papier

Une grille terminée^

Grilles d’analyse des séances expérimentées dans les classes en co-observation:

Analyse Loto CP

Analyse Loto CM

VIDÉOS (mot de passe: labomaths):

LBM D1 Classe de CP de Karine

LBM D2 Classe de CM1CM2 d’Isabelle

LABOMATHS

LaboMaths C

6 mai 2019 ogenelot

Nous avons choisi de travailler en résolution de problèmes avec un problème atypique ouvert∗, Des bananes dans le désert, qui peut être adapté selon le niveau des élèves:

Problème initial: Dans un désert d’une longueur de 1000 km, vous devez transporter 3000 bananes avec un dromadaire ne pouvant porter que 1000 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, quel est le plus grand nombre de bananes que vous pouvez apporter au bout du désert ?

Cycle 3: Dans un désert d’une longueur de 100 km, vous devez transporter 300 bananes avec un dromadaire ne pouvant porter que 100 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, quel est le plus grand nombre de bananes que vous pouvez apporter au bout du désert ?

Cycle 2 et 3: Dans un désert d’une longueur de 10 km, vous devez transporter 30 bananes avec un dromadaire ne pouvant porter que 10 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, comment faire pour emmener 4 bananes à l’autre bout du désert ?

Problèmes similaires avec une modélisation identique (multiprésentations):

Un écureuil change de cachette car elle est trop petite. Il faut qu’il emporte ses 300 noisettes dans sa nouvelle cachette située dans un arbre à 100 m. Il ne peut porter que 100 noisettes sur son dos mais étant gourmand il a besoin de manger une noisette par mètre parcouru. Quel est le plus grand nombre de noisettes qu’il peut emporter dans sa nouvelle cachette ?

Un kangourou doit emporter 300 kiwis à son petit de l’autre côté de la prairie. La prairie se traverse en 100 bonds. Il ne peut transporter que 100 kiwis dans sa poche mais à chaque bond il perd un kiwi qui s’écrase par terre. Quel est le plus grand nombre de kiwis entiers qu’il peut emporter à son petit ?

Problèmes adaptés au cycle 2 (CP) :

Au zoo, dans l’enclos du singe, il y a 4 arbres en ligne. Dans le premier arbre il y a 6 bananes. Le singe doit transporter 1 banane sur le dernier arbre. Mais attention ! Le singe ne peut porter que 3 bananes à la fois et à chaque fois qu’il fait un saut, il doit manger une banane pour prendre des forces ! Combien de bananes peut-il emporter sur le dernier arbre ?

Au zoo, dans l’enclos du singe, il y a 10 arbres en ligne. Dans le premier arbre il y a 20 bananes. Le singe doit transporter le plus de bananes sur le dernier arbre. Mais attention ! Le singe ne peut porter que 10 bananes à la fois et à chaque fois qu’il fait un saut, il doit manger une banane pour prendre des forces ! Combien de bananes peut-il emporter sur le dernier arbre ?

Dans la jungle, un singe veut ramener le plus possible de bananes. Il y a 20 bananes sur un bananier. Pour retourner chez lui, le singe doit sauter sur 10 rochers. Mais attention ! Le singe ne peut porter que 10 bananes à la fois et à chaque fois qu’il fait un saut, il doit manger une banane pour prendre des forces. Combien de bananes le singe peut-il emporter chez lui ?

Remarques importantes:

Ces problèmes sont difficiles à mettre en place dans les classes, de nombreux imprévus, souvent liés à l’interprétation des énoncés par les élèves, apparaissent au fur et à mesure des tests. Ces énoncés ont été modifiés très régulièrement au cours des expériences et nécessitent d’être testés à nouveau afin d’optimiser les séances.

∗ problème de type ouvert: on peut définir cette catégorie de problèmes comme des situations dont l’énoncé n’induit ni méthode ni application immédiate, mais dont le contexte est suffisamment familier des élèves pour qu’ils puissent entrer rapidement dans la recherche et faire des hypothèses. Ces problèmes peuvent avoir des solutions encore difficiles à prouver en mathématiques. Thierry Dias

Rappel des programmes corrigés 2018 :

« Aux cycles 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »

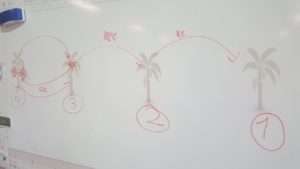
<Schématisation faite avec des CM1 (30 bananes dans le désert)

Schématisation test du problème 6 bananes pour le singe CP ^

Matériel:

Fiche de séance BANANES DANS LE DÉSERT

300 Bananes dans le désert C3

30 Bananes dans le désert C2C3

30 Bananes dans le désert C2 V2

plateau désert 10 km

plateau désert 100 km

Les 20 bananes

Les bananes du singe

Grilles d’analyse des séances expérimentées dans les classes en co-observation:

Grille Analyse BN CM

Grille analyse BN CP

Lien vers la solution du problème initial (désert de 1000km)

VIDÉOS (mot de passe: labomaths):

LBM C1 Classe de CM1 de Vincent

LBM C2 Classe de CP d’Anne-Sophie

LABOMATHS

LaboMaths B

6 mai 2019 ogenelot

Nous avons choisi de travailler en résolution de problèmes avec un problème atypique, Le triangle magique, que nous avons préparé afin de le proposer à des classes de cycle 2 (CE1/CE2, CP):

Placer les six nombres 1, 2, 3, 4, 5, 6 dans les cases pour que la somme des trois nombres soit égale à dix sur chacun des côtés du triangle.

Rappel des programmes corrigés 2018 :

« Au cycle 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »