Jeux mathématiques pour travailler les compléments

Domaines: numération et calcul mental

Lors de l’année 2018-2019, les enseignantes de l’ex-LaboMaths D avaient travaillé sur la numération de position, et notamment élaboré des jeux de Loto afin de consolider les notions de chiffre et de nombre chez des élèves de cycle 2 et 3. Cette année, les membres du groupe ont désiré poursuivre leur travail collaboratif en axant leur thématique autour du calcul mental et en travaillant plus précisément les compléments à dix et aux dizaines supérieures. Les jeux élaborés s’adressent à des élèves de cycle 2, mais les élèves de cycle 3 peuvent en bénéficier: renforcement pour des élèves en difficulté, consolidation pour les autres.

BO n° 30 du 26/07/2018 (extraits):

« La pratique quotidienne du calcul mental conforte la maîtrise des nombres et des opérations et permet l’acquisition d’automatismes procéduraux et la mémorisation de résultats comme ceux des compléments à 10, des tables d’addition et de multiplication. »

Repères annuels de progression du cycle 2:

Les élèves ont travaillé les compléments à l’aide de jeux de calcul mental élaborés par le Labomaths 2.3:

• le jeu Cache 10 inspiré du jeu Les Dix-minos (Ermel CE1)  testé en classe de CP et CE1.
• le jeu La Rivière aux Dizaines testé avec des petits groupes de CE2, CM1 et CM2.

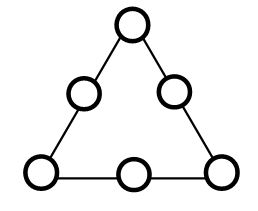
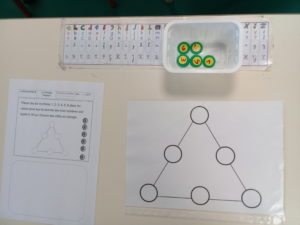
CACHE 10

pour travailler essentiellement  les compléments à dix (cycle 2)

GRILLE DE PRÉPARATION

OBSERVATION ANALYSE

Le jeu CACHE 10 niveaux 1 2 3

Le jeu CACHE 10 niveau 4

Le jeu CACHE 10 niveau 5

CACHE 10 RÈGLE DU JEU

Remarques:

• Attention au découpage des cartes: chacune doit regrouper deux cases (comme un domino).
• Prévoir 5 caches de chaque taille pour chaque élève et des couleurs différentes par joueur.
  

Cartes mémoire

EXERCICE: nombres croisés

Vidéo: Classes de CE1 CE2 de Magali et CE1 de Bénédicte (mot de passe labomaths71)

—————————-

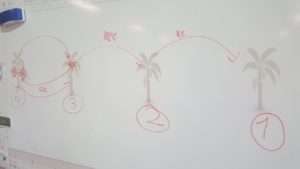
La Rivière aux Dizaines

pour travailler les compléments aux dizaines supérieures et le calcul mental (cycle 3)

La rivière aux dizaines

Règle du jeu Rivière aux dizaines

La schématisation

Domaine: résolution de problèmes

Après un travail conséquent sur les typologies de problèmes selon Catherine Houdement et Gérard Vergnaud, le groupe Labomaths s’est attardé sur la conférence de Serge Petit (professeur honoraire de mathématiques, IUFM d’Alsace) intitulée Résolution de problèmes et registres de représentations sémiotiques.

Après un visionnage attentif de cette conférence, entrecoupée d’échanges constructifs, le groupe a décidé d’orienter le travail du Labomaths vers la schématisation en RDP.  De nombreuses questions émergent: comment faire pour que le schéma soit un outil à la résolution de problèmes ? Comment l’introduire ? Quels problèmes travailler ? Problèmes basiques ? Complexes ? Faut-il se concentrer sur les problèmes qui mettent en jeu une chronologie, une notion de temps ? Certains élèves ont déjà des représentations schématiques, cela peut-il servir d’amorce pour en trouver d’autres ? Comment travailler les représentations sémiotiques dans les classes (CE et CM) ?

Lien vers le site de l’Académie des Sciences pour visionner la conférence de Serge Petit

En raison de l’épidémie de Covid 19 et de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.

Résolution d’un problème atypique

Les 99 carrés

Après un travail conséquent sur la catégorisation de problèmes selon Catherine Houdement et Gérard Vergnaud, les enseignant.e.s du Labomaths 2.1 ont choisi de faire résoudre un problème de recherche à leurs élèves, les 99 carrés, en s’inspirant des recherches faites par le laboratoire 3LS (Laboratoire Lausannois Lesson Study) dirigé par Stéphane Clivaz, professeur spécialiste de la didactique des mathématiques à la Haute École Pédagogique du canton de Vaud.

Rappel des programmes corrigés 2018 :

« Aux cycles 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »

Compte-rendu de la dernière réunion avant le confinement

Les 99 carrés

Plan leçon des 99 carrés, labo 3LS HEP Vaud

En raison de l’épidémie de Covid 19, de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.

PROJET BAR-NUM

Domaine: numération

Le jeu Bar-Num a été élaboré par les maîtres sur-numéraires de Chalon 2 à partir du jeu des « frites » (de piscine) proposé par la Méthode Heuristique des Maths (MHM) de Nicolas Pinel, Inspecteur de l’Education Nationale. Il permet de travailler les compositions et les décompositions des premiers nombres de 1 à 10 avec des élèves de cycle 1 et début cycle 2.

En raison de l’épidémie de Covid 19, de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce Labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.

Grandeurs et mesures: les masses

Comment travailler les représentations avec des unités non usuelles ?

Les enseignantes de ce groupe ont souhaité travailler les représentations des grandeurs et en particulier les masses. Elles remarquent régulièrement que leurs élèves ont des difficultés à se représenter ce qu’est un mètre, un kilomètre, un kilogramme, un litre, etc … Dans ce domaine, en cycle 2, on a tendance à travailler très vite avec les unités de mesures usuelles, alors que beaucoup d’élèves ont encore besoin de manipuler, de « voir », de « sentir », de « soupeser » ce que fait un kilogramme, de se rendre compte d’une distance « en vrai »,  de comparer différents objets en les soupesant, … Ce travail est la plupart du temps pratiqué en classe, mais peut-être pas suffisamment pour certains élèves.

Les enseignantes font remarquer que les élèves manipulent peu, qu’on va souvent trop vite pour répondre aux demandes institutionnelles. La manipulation est utile seulement si les élèves apprennent quelque chose, si elle a un objectif. On ne manipule pas sans but : attention au mode « énactif » ; la manipulation n’est pas un « jeu », elle doit permettre de faire émerger une notion, un savoir, d’où la difficulté pour trouver des situations qui permettent cette manipulation…

Le groupe décide de s’orienter plutôt vers les mesures de masses pour travailler les notions d’estimation et d’étalonnage avec des manipulations d’objets de masse identiques ou différentes, et des pesées avec des unités non usuelles. Le visionnage de l’intervention de Céline Mousset et d’Hélène Gagneux sur les grandeurs et mesures lors du colloque organisé par l’ Académie des Sciences en décembre 2018 a beaucoup aidé dans ce choix.

Lien vers le site de l’Académie des Sciences pour visionner la conférence d’Hélène Gagneux et Céline Mousset

Repères annuels : « Les élèves comparent des objets selon leur masse, en les soupesant puis en utilisant la balance à plateaux, type Roberval, sans que des unités de mesure soient nécessairement introduites. Ils donnent du sens aux expressions : « Plus lourd que, plus léger… ».

Attendus de fin de CP

Ce que sait faire l’élève:

– Il compare des objets selon leurs masses, en les soupesant (si les masses sont suffisamment distinctes) ou en utilisant une balance de type Roberval.

-Il utilise le lexique spécifique associé aux masses: plus lourd, moins lourd, plus léger.

Exemples de réussite: les situations s’appuient toutes sur des manipulations

Il compare les masses de deux objets par comparaison directe et indirecte à l’aide d’une balance.

Parmi deux ou trois bouteilles opaques d’apparence identique, mais remplies différemment (l’objectif est qu’elles aient des masses différentes), il sait dire laquelle est la plus lourde ou laquelle est la plus légère.

Attendus de fin de CE1 et de CE2

Il sait identifier l’objet le plus léger (ou le plus lourd) parmi 2 ou 3 objets de volume comparable en les soupesant ou en utilisant une balance.

Il compare des masses par comparaison directe et indirecte à l’aide d’une balance.

Il estime un ordre de grandeur en référence à certains objets du quotidien.

Pour comparer deux masses, il utilise le vocabulaire approprié.

Compte-rendu de la dernière réunion du Labomaths avant le confinement

En raison de l’épidémie de Covid 19 et de la fermeture des écoles de mars à mai 2020, et du protocole sanitaire mis en place dans les écoles lors de la réouverture des classes, il n’a pas été possible de continuer ce labomaths. Il sera repris pendant l’année scolaire 2020-2021 si les conditions le permettent.

PROJET AVDV (Application Verger De Village)

Domaines: Résolution de problèmes, grandeurs et mesures

Le projet initial du Labomaths 1.2 était de travailler la résolution de problèmes à partir de données issues du terrain, le verger du village de La Charmée, où de nombreux arbres fruitiers sont visités régulièrement par les élèves du RPI regroupant les écoles de Granges, Saint Germain-les-Buxy et La Charmée.

A partir de mesures prises dans le verger, les élèves de cycle 2 et 3 auraient dû résoudre des problèmes correspondant à leurs niveaux de classe. En raison de l’épidémie de covid 19 et de la fermeture des écoles en mars 2020, nous n’avons pas pu finaliser le projet. Seules les mesures sur le terrain et leur exploitation dans les classes ont été réalisées, ce qui a déjà demandé beaucoup de temps de préparation et d’organisation.  Les enseignant.e.s envisageaient de faire résoudre un problème de recherche aux élèves de chaque cycle à partir d’une commande fictive de la mairie. Cette commande se serait présentée sous forme d’une lettre précisant que la municipalité souhaitait entourer le verger d’un grillage, avec un portillon et un portail. Les élèves auraient été chargés de réaliser un devis à l’aide de catalogues papier ou en ligne, puis d’écrire un problème collectif dans le but de le proposer à une classe d’une autre commune. Cette phase n’a pu être réalisée, les conditions de réouverture des écoles en mai 2020 n’étaient pas propices à ce type de travail qui aurait demandé une coopération étroite entre élèves. En accord avec les enseignant.e.s, cette phase sera reportée au premier trimestre de l’année scolaire 2020-2021.

Les données recueillies sur le terrain ont été transmises à deux étudiants de l’IUT de Chalon afin qu’ils réalisent une application en réalité virtuelle dans le cadre de leur parcours de master.

Voir le projet pensé au niveau des étudiants

BO n° 30 du 26/07/2018 (extraits):

« Au cycle 2, la résolution de problèmes est au centre de l’activité mathématiques des élèves […]. Les problèmes […] peuvent être issus de situations de vie de classe ou de situations rencontrées dans d’autres enseignements, notamment « Questionner le monde », ce qui contribue à renforcer le lien entre les mathématiques et les autres disciplines. […] L’étude des quatre opérations commence dès le début du cycle à partir de problèmes qui contribuent à leur donner du sens, en particulier des problèmes portant sur des grandeurs ou sur leurs mesures. […] En lien avec le travail mené dans « Questionner le monde » les élèves rencontrent des grandeurs qu’ils apprennent à mesurer […]. L’étude des grandeurs et de leurs mesures doit faire l’objet d’un enseignement structuré et explicite qui s’appuie sur des situations de manipulation. »

Repères annuels de progression Grandeurs et mesures pour le cycle 2:

BO n° 25 du 21/06/2018:

« Dans la continuité des cycles précédents, le cycle 3 assure la poursuite du développement des six compétences majeures des mathématiques: chercher, modéliser, représenter, calculer, raisonner et communiquer. La résolution de problèmes constitue le critère principal de la maîtrise des connaissances dans tous les domaines des mathématiques […]. Les situations sur lesquelles portent les problèmes sont, le plus souvent, issues de la vie de classe, de la vie courante ou d’autres enseignements, ce qui contribue à renforcer le lien entre les mathématiques et les autres disciplines. »

Repères annuels de progression Grandeurs et mesures pour le cycle 3:

Le plan du verger

Cycle 3

Cycle 2

Phase 2 du projet: résolution de problème à partir d’une commande fictive de la mairie

Vidéo: mesure de distances entre les arbres avec deux petites cordes identiques par des CP CE1:

Domaine: Résolution de problèmes

Objectif Dix

La résolution de problème est la thématique du groupe. Nous avons choisi de travailler les analogies entre problèmes en se basant sur les préconisations en RDP d’instituer 10 problèmes par semaine sur l’ensemble de la scolarité élémentaire. Nous avons été inspirés par les travaux réalisés par Nicolas Naulin (PEMF) dans sa classe de CM2 dans la circonscription de Charolles (merci à lui pour ses conseils et informations diverses !) et avons souhaité adapter son procédé à des classes de cycle 2 (CP, CE1 et CE2). Devant l’ampleur du travail, nous avons tout d’abord construit un protocole sur une semaine type avant de l’enrichir progressivement pour tenter de couvrir quatre semaines selon une programmation basée sur les différentes typologies de problèmes (selon G. Vergnaud et C. Houdement). Un travail approfondi sur les énoncés des problèmes a été mené en s’inspirant des travaux de Stella Baruk et Serge Petit. Lors des résolutions, les élèves ont été initiés à la schématisation de problèmes basiques: certains schémas leur ont été proposés par les enseignantes, d’autres viennent des élèves eux-mêmes.

Le protocole Objectif 10:

Lundi:  un problème de référence (résolution / institutionnalisation)

Mardi: trois problèmes dont un problème analogue à celui du lundi (contexte identique au lundi, données numériques différentes)

Jeudi: trois problèmes dont un problème analogue à celui du lundi (contextes différents, données numériques identiques au lundi)

Vendredi: trois problèmes dont un problème analogue à celui du lundi (contextes différents, données numériques différentes)

BO n° 30 du 26/07/2018 (extrait):

« Au cycle 2, la résolution de problèmes est au centre de l’activité mathématiques des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions, de provoquer des questionnements. Ils peuvent être issus de situations de vie de classe ou de situations rencontrées dans d’autres enseignements, notamment « questionner le monde », ce qui contribue à renforcer le lien entre les mathématiques et les autres disciplines. Il ont le plus souvent possible un caractère ludique. […] »

Exemples de schémas de CE1

Exemples de schémas de CE2

GRILLE PRÉPARATION  CP

GRILLE PRÉPARATION  CE1CE2

GRILLE OBSERVATION ANALYSE  CP

GRILLE OBSERVATION ANALYSE  CE1

GRILLE OBSERVATION ANALYSE CE2

LA SCHEMATISATION EN CYCLE 2

Quatre semaines de problèmes en CP

Quatre semaines de problèmes en CE1

Quatre semaines de problèmes en CE2

En raison de l’épidémie de COVID 19 et de la fermeture des écoles en mars 2020, les problèmes n’ont pas tous été testés dans les différentes classes. Il se peut que certains de ces problèmes, notamment ceux des semaines 4, aient besoin d’ajustements, ajustements qui auraient dû se faire à la suite des tests dans les classes.

Nous avons choisi de consolider la numération décimale de position et la signification de la place des chiffres dans les nombres inférieurs à 1000 ( dans 108, il n’y a pas 0 dizaine mais 10 dizaines , distinction entre le chiffre des … et le nombre de … ) en privilégiant le cycle 2.  Deux jeux différents ont été testés dans des classes de CP, CE et CM: le jeu de Loto Coopératif et le jeu du manège (adaptation du jeu de la toupie élaboré par le laboratoire 3LS de la HEP de Lausanne).

Rappel des programmes corrigés 2018:

« Au cycle 2, les élèves consolident leur compréhension des nombres entiers, déjà rencontrés au cycle 1. Ils étudient différentes manières de désigner les nombres, notamment leurs écritures en chiffres, leurs noms à l’oral, les compositions-décompositions fondées sur les propriétés numériques, ainsi que les décompositions en unités de numération (unités, dizaines, etc.). »

Tout en privilégiant la manipulation, la verbalisation et l’abstraction, nous avons pris soin de proposer des pistes de remédiation et d’extension afin que chaque élève puisse évoluer selon son rythme.

Matériel:

Fiche de séance LE LOTO COOPERATIF

>LOTO DES CP  EXERCICES LOTO CP

>LOTO DES CEEXERCICES LOTO CE

>LOTO DES CM EXERCICES LOTO CM

>Jeu du manège CP >Jeu du manège CECM

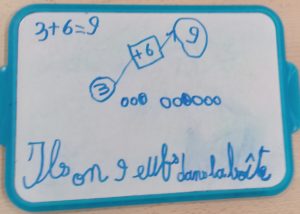
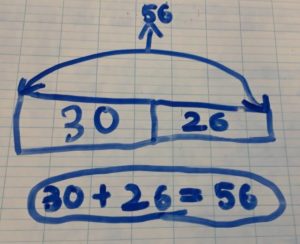
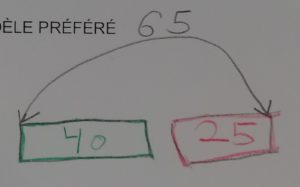
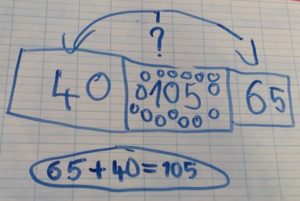
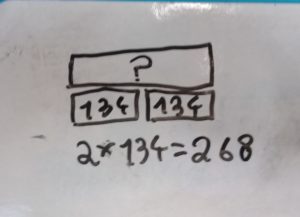
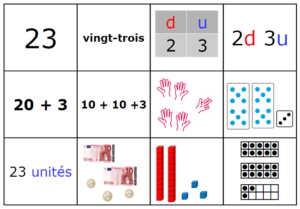
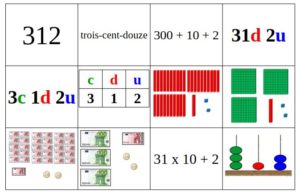
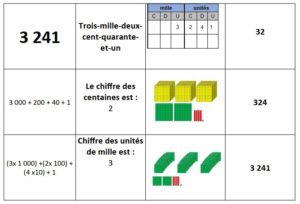
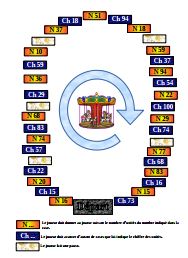
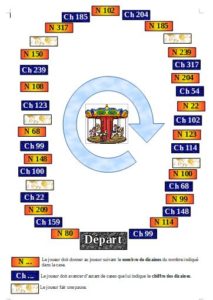
Matériel de numération version papier avec la grille grand format^

Matériel numération version papier

Une grille terminée^

Grilles d’analyse des séances expérimentées dans les classes en co-observation:

Analyse Loto CP

Analyse Loto CM

VIDÉOS (mot de passe: labomaths):

LBM D1 Classe de CP de Karine

LBM D2 Classe de CM1CM2 d’Isabelle

Nous avons choisi de travailler en résolution de problèmes avec un problème atypique ouvert∗, Des bananes dans le désert, qui peut être adapté selon le niveau des élèves:

Problème initial: Dans un désert d’une longueur de 1000 km, vous devez transporter 3000 bananes avec un dromadaire ne pouvant porter que 1000 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, quel est le plus grand nombre de bananes que vous pouvez apporter au bout du désert ?

Cycle 3: Dans un désert d’une longueur de 100 km, vous devez transporter 300 bananes avec un dromadaire ne pouvant porter que 100 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, quel est le plus grand nombre de bananes que vous pouvez apporter au bout du désert ?

Cycle 2 et 3: Dans un désert d’une longueur de 10 km, vous devez transporter 30 bananes avec un dromadaire ne pouvant porter que 10 bananes sur son dos. En sachant qu’il consomme 1 banane par kilomètre parcouru, comment faire pour emmener 4 bananes à l’autre bout du désert ?

Problèmes similaires avec une modélisation identique (multiprésentations):

Rappel des programmes corrigés 2018 :

« Aux cycles 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »

Tout en privilégiant la manipulation, la verbalisation et l’abstraction, nous avons pris soin de proposer des pistes de remédiation et d’extension afin que chaque élève puisse évoluer selon son rythme.

<Schématisation faite avec des CM1 (30 bananes dans le désert)

Schématisation test du problème 6 bananes pour le singe CP ^

Matériel:

Fiche de séance BANANES DANS LE DÉSERT

300 Bananes dans le désert C3

30 Bananes dans le désert C2C3

30 Bananes dans le désert C2 V2

plateau désert 10 km

plateau désert 100 km

Les 20 bananes

Les bananes du singe

Grilles d’analyse des séances expérimentées dans les classes en co-observation:

Grille Analyse BN CM

Grille analyse BN CP

Lien vers la solution du problème initial (désert de 1000km)

VIDÉOS (mot de passe: labomaths):

LBM C1 Classe de CM1 de Vincent

LBM C2 Classe de CP d’Anne-Sophie

Nous avons choisi de travailler en résolution de problèmes avec un problème atypique, Le triangle magique, que nous avons préparé afin de le proposer à des classes de cycle 2 (CE1/CE2, CP):

Placer les six nombres 1, 2, 3, 4, 5, 6 dans les cases pour que la somme des trois nombres soit égale à dix sur chacun des côtés du triangle.

Rappel des programmes corrigés 2018 :

« Au cycle 2 et 3, la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer. Les problèmes permettent d’aborder de nouvelles notions, de consolider des acquisitions […]. On veillera à proposer aux élèves dès le CP des problèmes pour apprendre à chercher qui ne soient pas de simples problèmes d’application à une ou plusieurs opérations mais nécessitent des recherches avec tâtonnements. »

Tout en privilégiant la manipulation, la verbalisation et l’abstraction, nous avons pris soin de proposer des pistes de remédiation et d’extension afin que chaque élève puisse évoluer selon son rythme.

Matériel:

Fiche de séance Le triangle magique

Plateau jeu triangle magique

Énoncé triangle magique

Énoncé carré magique

Bandes 3 cases

Trace écrite CE

Trace écrite CP

Grilles d’analyse des séances expérimentées dans les classes en co-observation:

Grille prépa analyse TM CE

Grille prépa analyse TM CP

Quelques idées (merci JM Guillemeney)

VIDÉOS (mot de passe: labomaths):

LBM B1 Classe de CE1/CE2 d’Elisabeth

LBM B2 Classe de CP d’Yvon